How do I use the functional form of @ (at) apply?
Short answer:
1. @[container; indices; function]
2. @[container; indices; function; second_args]
(Note that there is another overload for @ with three arguments, called protected execution, which is invoked when the first argument to @ is a function or projection; protected execution is discussed in another faq.)
In the 3-argument case, q applies function to those elements of container specified by indices, leaving the rest of container alone. In other words, the behavior of 3-argument @ (apply) resembles that of the following function:
Although this model breaks down when the first argument is a global variable name, it is very helpful in understanding what is going on even in that case. Let’s look at a couple of simple examples to clarify this:
q)list: 1 + til 8
q)list
1 2 3 4 5 6 7 8
q)@[list; 0; neg] / negate element 0
-1 2 3 4 5 6 7 8
q)list / list remains unmodified
1 2 3 4 5 6 7 8
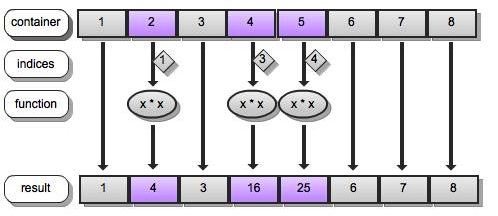
q)@[list; 1 3 4; {x * x}] / square elements 1, 3, and 4
1 4 3 16 25 6 7 8
q)
The diagram below illustrates the last example above:
Because the new container has the same type and shape as the original, function must return the same type as its argument, unless the container is a mixed list (i.e., type 0):
q)@[list; 4 5 6 7; {x div 2}] / list is an int list
1 2 3 4 2 3 3 4
q)@[list; 4 5 6 7; {x % 2}] / but % returns float
'type
q)mixed_list: 1 2, `3`4
q)type mixed_list
0h
q)@[mixed_list; 0 3; string] / anything goes with type 0
,"1"
2
`3
,"4"
q)
Next, we’ll consider the second case listed at the top of this faq. When function is dyadic and a fourth argument is supplied, @ (apply) behaves like the following function:
The basic idea is still the same, i.e., to transform selected elements while leaving the rest of the container intact. The difference is that, instead of function being modified by each, it is modified by ‘(each-both) (also see this faq on each-both and multivalent each), so that the selected elements of container are paired up with the corresponding elements from second_args:
q)@[list; 1 3 5 7; +; 10 20 30 40]
1 12 3 24 5 36 7 48
q)@[list; (1 3 5 7; 0 2 4 6); *; 2 -2]
-2 4 -6 8 -10 12 -14 16
q)
One function often used with 4-argument @ (apply), is : (amend). We can replace selected elements with a certain value (or values) as follows:
q)list: 1 + til 8
q)@[list; 1 3 5 7; :; 47]
1 47 3 47 5 47 7 47
q)@[list; 1 3 5 7; :; 10 20 30 40]
1 10 3 20 5 30 7 40
q)
It might appear that the above example exposes a flaw in our model, apply_dyadic, of @ (apply). However, recall that, when modified by an adverb, : (amend) does not modify its first argument:
q):'[list 1 2 3; 20 30 40]
20 30 40 / :' returns its 2nd argument
q)list / without modifying its 1st
1 2 3 4 5 6 7 8
q)
Where our models do break down is when, as alluded to earlier, the first argument is the name of global variable referring to a container, rather than the value of a container. In that case, the mechanics of the operation are the same, but original container is modified, and the return value is the name:
q)list: 1 + til 8
q)@[`list; 0; neg]
`list
q)list
-1 2 3 4 5 6 7 8
q)
This behavior is handy for writing functions of your own that work in both scenarios – either creating a new value or modifying one in place – like the following:
We can also use @ to apply a function to selected entries in a dictionary:
q)dictionary: `a`b`c`d ! `1`2, 3 4
q)dictionary
a| `1
b| `2
c| 3
d| 4
q)@[dictionary; `a`b; {"I"$ string x}]
a| 1
b| 2
c| 3
d| 4
q)
Tables can be transformed as well. Consider the following table:
q)t: ([] col1: `foo`bar`baz; col2: 5 10 15f)
q)t
col1 col2
---------
foo 5
bar 10
baz 15
q)
Recall that each row of a table is a dictionary:
q)t 0
col1| `foo
col2| 5f
q)
Thus, we can use @ (apply) to accomplish an update in the following manner:
q)update col2 - 4 from t where i > 0
col1 col2
---------
foo 5
bar 6
baz 11
q)@[t; 1 2; {[row] row[`col2] -: 4; row}]
col1 col2
---------
foo 5
bar 6
baz 11
q)
We could also obtain the previous result using nested calls to @ (apply):
q)@[t; 1 2; @[; `col2; -[; 4]]]
col1 col2
---------
foo 5
bar 6
baz 11
q)
Since we can index tables using column names, we can double all of the entries in col2 as follows:
q)@[t; `col2; 2*]
col1 col2
---------
foo 10
bar 20
baz 30
q)